斜面上を滑る物体の速度変化をグラフにしてみよう
このページでは、高校物理で学ぶ「斜面上を滑る物体の運動」をテーマに、 斜面の角度・質量の条件を変えたときの違いを 桜チャートで可視化していきます。
自由落下と同様に、斜面上を滑る物体も等加速度運動をしますが、 ここでは摩擦なし(μ = 0)のシンプルな場合に絞って、 「質量を変えたとき」「角度を変えたとき」の違いをグラフで比べます。
1. 斜面上の運動の基本式
斜面角度を θ とすると、摩擦がない場合の斜面方向の加速度は次の式で表されます。
a = g \* sinθ
ここで、g は重力加速度(9.8 [m/s²])です。
式の中に質量 m が登場しないため、質量を変えても加速度は同じになります。
これをグラフにすると、異なる質量の曲線がきれいに重なることが分かります。
2. 今回のサンプルデータの条件
- 時間:
t = 0.0 ~ 2.0 [s](0.2刻み) - 斜面角度:
- 質量ぶり:
30°固定 - 角度ぶり:
20°・30°・40°
- 質量ぶり:
- 摩擦係数:
μ = 0(摩擦なし) - 質量:
1[kg], 3[kg], 5[kg]
速度と位置は等加速度運動の公式で計算しています。
v(t) = a t
x(t) = (1/2) a t²
3. グラフ比較(質量ぶり)
まずは、斜面の角度を 30° に固定し、質量だけを変えたときの速度変化を比較します。
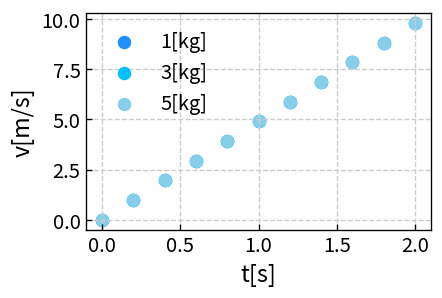
図1:質量 1[kg], 3[kg], 5[kg] の速度変化(角度30°、摩擦なし)。3本とも完全に一致する。
1[kg], 3[kg], 5[kg] のどの場合でも、速度の増え方が同じになっていることが分かります。 これは、斜面方向の力学方程式で質量が打ち消しあうためです。 「重い物体は力も大きいが、その分動きにくい」ので、結果として同じ加速度になると理解できます。
4. グラフ比較(角度ぶり)
次に、質量を 1[kg] に固定し、斜面の角度を変えたときの速度変化を比較します。
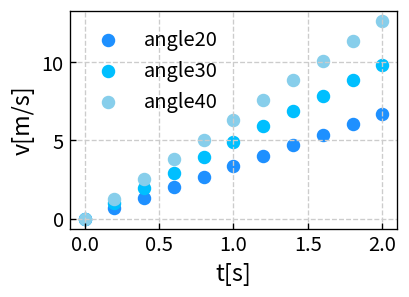
図2:角度20°・30°・40°の速度変化(質量1[kg]、摩擦なし)。角度が大きいほど立ち上がりが急になる。
角度が大きくなるほど sinθ が大きくなり、加速度も大きくなります。
同じ時間でも速度がより大きくなるため、グラフの傾きが急になります。
5. サンプルデータ(CSV)
下のボタンから、それぞれのサンプルデータをコピーできます。 テキストエディタや Excel に貼り付けて CSV として保存し、桜チャートに読み込んでください。
5-1. 質量ぶり(mass_compare.csv)
斜面角度30°・摩擦なしの場合に、質量を 1[kg], 3[kg], 5[kg] と変えたデータです。
5-2. 角度ぶり(angle_compare.csv)
質量1[kg]・摩擦なしの場合に、斜面角度を 20°・30°・40° と変えたデータです。
6. まとめ
- 斜面角度が大きくなるほど加速度は大きくなり、速度の立ち上がりが急になる。
- 摩擦がない場合、斜面上の運動でも質量によらず同じ加速度で運動する。
- 桜チャートを使うと、「質量ぶり」と「角度ぶり」を簡単に切り替えて比較できる。
自由落下と合わせて、斜面運動もグラフで眺めると物理のイメージがかなり掴みやすくなります。 条件を変えたオリジナルのデータも作って、ぜひいろいろ試してみてください。