初速度ありの自由落下――投げ下ろすと、自由落下はどう変わるのか?(空気抵抗なし)
「自由落下」という言葉から、多くの人は静かに手を離して物体を落とす状況を思い浮かべるでしょう。
しかし実際の運動には、もう一つの重要なケースがあります。それが下向きに投げてから落とす(投げ下ろし)場合です。
本記事では、空気抵抗がない理想的な条件を前提として、初速度を持った自由落下の運動を考えます。
同じ高さから落とすのに、そっと離した場合・軽く投げ下ろした場合・強く投げ下ろした場合で、
どこが同じで、どこが違うのかを、速度と距離のグラフで整理します。
1. 前提条件(重要)
この記事のモデルは、次のような理想条件を置いています。
- 空気抵抗はない(真空を想定)
- 物体の形・大きさは考えない
- 重力加速度は一定
- 落下方向は鉛直下向き
現実の世界では空気抵抗の影響を受けますが、ここでは自由落下の基本構造を理解するために単純化しています。
2. 初速度を持った自由落下とは
通常の自由落下は、落とした瞬間の速度(初速度)が 0 です。
投げ下ろしでは、落下開始時点ですでに速度を持っています。この「最初に持っている速度」を初速度と呼びます。
v(t) = v0 + g t
x(t) = v0 t + (1/2) g t²
ここで重要なのは、初速度が変わっても、重力加速度 g は同じという点です。
「強く投げたから、より強い重力が働く」ということはありません。
3. よくある誤解:「速くなる=加速度が大きい」?
初速度ありの自由落下では、速さと加速度が混同されがちです。
- 投げ下ろした方が速く落ちる → これは正しい
- 投げ下ろした方が加速度が大きい → これは誤り
実際に起きているのは、加速度は同じ(g)で、ただスタート地点の速度が違うだけです。
たとえば、次の3つを比べても、どれも「同じ g」で加速します。
- 自由落下(v0 = 0)
- 軽く投げ下ろす(v0 = 5 m/s)
- 強く投げ下ろす(v0 = 10 m/s)
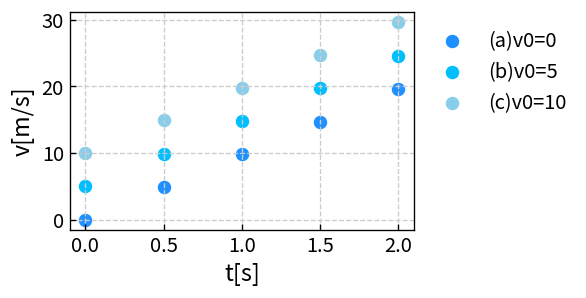
4. 速度グラフで見る初速度の影響
速度 v を縦軸、時間 t を横軸にしてグラフを描くと、特徴がはっきり現れます。
- すべて直線
- 傾きはすべて同じ(= g)
- 初速度が大きいほど、上に平行移動した直線
文章だけでは理解しづらい部分ですが、グラフにすると一目瞭然です。
桜チャートでは、LEVEL 列で v0 の違いを色分けして、同じグラフに重ねて確認できます。
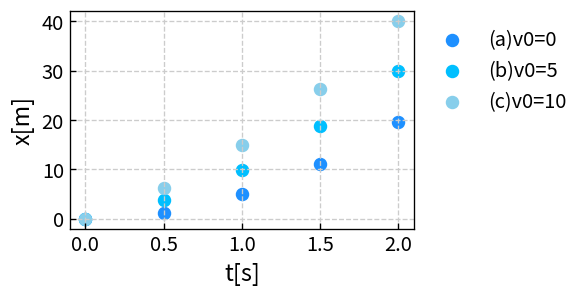
5. 距離グラフでは何が変わるのか
次に、縦軸を落下距離 x に切り替えると、グラフは放物線になります。
- すべて同じ曲がり具合(同じ加速度)
- 初速度が大きいほど、常に上側に位置する
速度グラフでは「平行な直線」でしたが、距離グラフでは「上下にずれた放物線」になります。
同じ CSV でも、Y軸を速度にするか距離にするかで見え方が変わる点は、グラフ学習の大きなポイントです。
6. なぜ差は最後まで縮まらないのか
「最初に速くても、いずれ追いつかれるのでは?」と感じる人もいるかもしれません。
しかし初速度の差は、時間が経っても消えません。
理由は単純で、すべて同じ加速度で加速しているので、速いものはその分だけ常に先に進むからです。
これは、速度グラフでは「平行な直線」、距離グラフでは「離れたままの放物線」として表れます。
7. 桜チャートでの確認方法
このテーマは桜チャートでの確認にとても向いています。
- X軸:
t[s] - Y軸:速度を見る →
v[m/s]/ 距離を見る →x[m] - LEVEL:
LEVEL(v0 の違い)
同じ CSV を使いながら、Y軸だけ切り替えると、速度(直線)と距離(放物線)の両方を確認できます。
8. サンプルデータ(Copy CSV)
下のボタンを押すと、桜チャートにそのまま貼り付けて使えるサンプル CSV をコピーできます。
(ページ上には生データを表示しません)
まずは速度グラフ(Y=v[m/s])で「平行な直線」を確認し、その後に距離グラフ(Y=x[m])に切り替えるのがおすすめです。
まとめ
- 本記事は空気抵抗がない理想条件を前提としている
- 初速度があっても、重力加速度は同じ
- 速度グラフは「平行な直線」になる
- 距離グラフは「上下にずれた放物線」になる
- 「速い」と「加速している」は別の概念
初速度あり自由落下は、文章だけだと誤解しやすいテーマですが、グラフで見ると理解が一気に進みます。
ぜひ桜チャートで、LEVEL と軸切り替えを試してみてください。