自由落下と空気抵抗：なぜ重い物体の方が速く落ちると感じるのか？

本記事では、空気抵抗がない場合と空気抵抗がある場合の自由落下を比較し、「重い物体ほど速く落ちるように感じる理由」を桜チャートのグラフを通して考えていきます。

ポイントは、空気抵抗がないときでも実際に 1kg / 5kg / 10kg の 3 本の線を用意して重ねることです。そうすることで、「本当に 3 本ともぴったり同じ線になる＝重さに依存していない」という事実を視覚的に確認できます。

1. 空気抵抗がない場合：重さを変えても同じ軌道をたどる

まず「空気が存在しない理想環境（真空）」を考えます。この場合、物体には重力のみが働き、すべての物体は同じ重力加速度

g = 9.8 m/s²

で落下します。重さ 1kg・5kg・10kg の物体を落としても、それぞれの速度は次の式で表せます。

v(t) = g t
x(t) = (1/2) g t²

ここで意図的に、「1kg」「5kg」「10kg」の 3 つの質量ラベル（LEVEL）を用意しつつ、計算式はすべて同じにしています。桜チャートで LEVEL 列に質量を指定すると、3 本のグラフが完全に重なって 1 本の直線に見えるはずです。

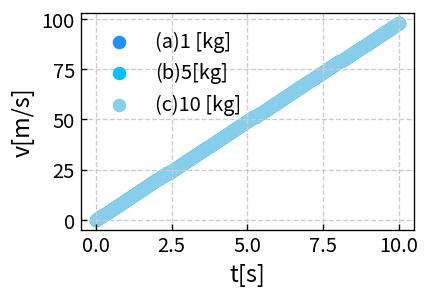
空気抵抗がない場合の自由落下 — 図1 空気抵抗がない場合の重さによる自由落下の速度変化の比較（3 本重ねても同じ線になる）

2. 地球ではなぜ「重い物体の方が速く落ちる」と感じるのか？

現実の地球上には空気が存在します。空気は動く物体に対して、常に空気抵抗（抗力）を与えます。

空気抵抗のおおまかな特徴は次の通りです。

物体の速度が速いほど大きくなる
物体の形・断面積によって大きさが変わる
軽い物体ほど同じ抵抗でも減速効果が大きい

同じような大きさ・形の物体であれば、軽い物体は空気抵抗の影響を強く受けてすぐに減速し、重い物体はそれほど減速されないため、結果として「重い方が速く落ちる」ように見えます。

有名な「月面でのハンマーと羽の実験」では、空気がほとんどない月で、ハンマーと羽を同時に落としてもまったく同じ速さで落下しました。これは、地球での感覚が空気抵抗によるものであることを示しています。

3. 空気抵抗がある場合：重さによってグラフが分かれてくる

空気抵抗を考慮した自由落下は、例えば次のような「速度に比例する抵抗」を仮定したモデルで表せます。

dv/dt = g - (k/m) · v

g：重力加速度
m：物体の質量（1kg, 5kg, 10kg）
k：空気抵抗係数

右辺の抵抗項 (k/m) · v は、質量が大きいほど小さくなるため、軽い物体は空気抵抗の影響を受けやすく、重い物体は受けにくいという性質がそのまま式に現れています。

実際に 1kg, 5kg, 10kg で計算した結果を桜チャートでプロットすると、空気抵抗がある場合には 3 本の線がきれいに分かれて表示されます。

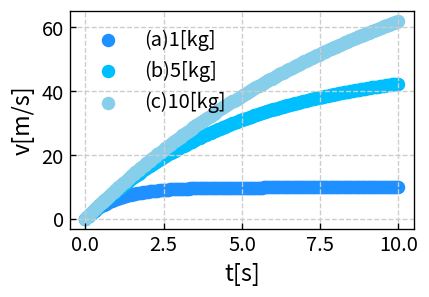
図2 空気抵抗がある場合の自由落下の重さによる違い（質量ごとに異なるカーブになる）

図1と図2を見比べると、 「空気抵抗がないときは 3 本が完全に重なる」のに対して、 「空気抵抗があるときは質量ごとに違うカーブになる」ことが分かります。

4. サンプルデータ（コピー式・空気抵抗なし／ありで分離）

ここからは、桜チャートにそのまま貼り付けて使えるデータを紹介します。 空気抵抗なしと空気抵抗ありで CSV を分けており、どちらもワンクリックでコピーできるようにしてあります。

列の定義は共通です：

t[s]：時間（秒）
v[m/s]：速度
x[m]：落下距離
LEVEL[kg]：質量ラベル（1, 5, 10）

桜チャートでは、例えば次のように指定して使う想定です。

速度グラフ：X 軸 = t[s], Y 軸 = v[m/s], LEVEL = LEVEL[kg]
位置グラフ：X 軸 = t[s], Y 軸 = x[m], LEVEL = LEVEL[kg]

4-1. 空気抵抗なし（3 水準が完全に重なるデータ）

下のボタンを押すと、空気抵抗なし（1kg, 5kg, 10kg）のサンプルデータがクリップボードにコピーされます。ページ上には生データは表示されません。

t[s]	v[m/s]	x[m]	LEVEL[kg]
0	0	0	(a)1 [kg]
0.05	0.49	0.01225	(a)1 [kg]
0.1	0.98	0.049	(a)1 [kg]
0.15	1.47	0.11025	(a)1 [kg]
0.2	1.96	0.196	(a)1 [kg]
0.25	2.45	0.30625	(a)1 [kg]
0.3	2.94	0.441	(a)1 [kg]
0.35	3.43	0.60025	(a)1 [kg]
0.4	3.92	0.784	(a)1 [kg]
0.45	4.41	0.99225	(a)1 [kg]
0.5	4.9	1.225	(a)1 [kg]
0.55	5.39	1.48225	(a)1 [kg]
0.6	5.88	1.764	(a)1 [kg]
0.65	6.37	2.07025	(a)1 [kg]
0.7	6.86	2.401	(a)1 [kg]
0.75	7.35	2.75625	(a)1 [kg]
0.8	7.84	3.136	(a)1 [kg]
0.85	8.33	3.54025	(a)1 [kg]
0.9	8.82	3.969	(a)1 [kg]
0.95	9.31	4.42225	(a)1 [kg]
1	9.8	4.9	(a)1 [kg]
1.05	10.29	5.40225	(a)1 [kg]
1.1	10.78	5.929	(a)1 [kg]
1.15	11.27	6.48025	(a)1 [kg]
1.2	11.76	7.056	(a)1 [kg]
1.25	12.25	7.65625	(a)1 [kg]
1.3	12.74	8.281	(a)1 [kg]
1.35	13.23	8.93025	(a)1 [kg]
1.4	13.72	9.604	(a)1 [kg]
1.45	14.21	10.30225	(a)1 [kg]
1.5	14.7	11.025	(a)1 [kg]
1.55	15.19	11.77225	(a)1 [kg]
1.6	15.68	12.544	(a)1 [kg]
1.65	16.17	13.34025	(a)1 [kg]
1.7	16.66	14.161	(a)1 [kg]
1.75	17.15	15.00625	(a)1 [kg]
1.8	17.64	15.876	(a)1 [kg]
1.85	18.13	16.77025	(a)1 [kg]
1.9	18.62	17.689	(a)1 [kg]
1.95	19.11	18.63225	(a)1 [kg]
2	19.6	19.6	(a)1 [kg]
2.05	20.09	20.59225	(a)1 [kg]
2.1	20.58	21.609	(a)1 [kg]
2.15	21.07	22.65025	(a)1 [kg]
2.2	21.56	23.716	(a)1 [kg]
2.25	22.05	24.80625	(a)1 [kg]
2.3	22.54	25.921	(a)1 [kg]
2.35	23.03	27.06025	(a)1 [kg]
2.4	23.52	28.224	(a)1 [kg]
2.45	24.01	29.41225	(a)1 [kg]
2.5	24.5	30.625	(a)1 [kg]
2.55	24.99	31.86225	(a)1 [kg]
2.6	25.48	33.124	(a)1 [kg]
2.65	25.97	34.41025	(a)1 [kg]
2.7	26.46	35.721	(a)1 [kg]
2.75	26.95	37.05625	(a)1 [kg]
2.8	27.44	38.416	(a)1 [kg]
2.85	27.93	39.80025	(a)1 [kg]
2.9	28.42	41.209	(a)1 [kg]
2.95	28.91	42.64225	(a)1 [kg]
3	29.4	44.1	(a)1 [kg]
3.05	29.89	45.58225	(a)1 [kg]
3.1	30.38	47.089	(a)1 [kg]
3.15	30.87	48.62025	(a)1 [kg]
3.2	31.36	50.176	(a)1 [kg]
3.25	31.85	51.75625	(a)1 [kg]
3.3	32.34	53.361	(a)1 [kg]
3.35	32.83	54.99025	(a)1 [kg]
3.4	33.32	56.644	(a)1 [kg]
3.45	33.81	58.32225	(a)1 [kg]
3.5	34.3	60.025	(a)1 [kg]
3.55	34.79	61.75225	(a)1 [kg]
3.6	35.28	63.504	(a)1 [kg]
3.65	35.77	65.28025	(a)1 [kg]
3.7	36.26	67.081	(a)1 [kg]
3.75	36.75	68.90625	(a)1 [kg]
3.8	37.24	70.756	(a)1 [kg]
3.85	37.73	72.63025	(a)1 [kg]
3.9	38.22	74.529	(a)1 [kg]
3.95	38.71	76.45225	(a)1 [kg]
4	39.2	78.4	(a)1 [kg]
4.05	39.69	80.37225	(a)1 [kg]
4.1	40.18	82.369	(a)1 [kg]
4.15	40.67	84.39025	(a)1 [kg]
4.2	41.16	86.436	(a)1 [kg]
4.25	41.65	88.50625	(a)1 [kg]
4.3	42.14	90.601	(a)1 [kg]
4.35	42.63	92.72025	(a)1 [kg]
4.4	43.12	94.864	(a)1 [kg]
4.45	43.61	97.03225	(a)1 [kg]
4.5	44.1	99.225	(a)1 [kg]
4.55	44.59	101.44225	(a)1 [kg]
4.6	45.08	103.684	(a)1 [kg]
4.65	45.57	105.95025	(a)1 [kg]
4.7	46.06	108.241	(a)1 [kg]
4.75	46.55	110.55625	(a)1 [kg]
4.8	47.04	112.896	(a)1 [kg]
4.85	47.53	115.26025	(a)1 [kg]
4.9	48.02	117.649	(a)1 [kg]
4.95	48.51	120.06225	(a)1 [kg]
5	49	122.5	(a)1 [kg]
5.05	49.49	124.96225	(a)1 [kg]
5.1	49.98	127.449	(a)1 [kg]
5.15	50.47	129.96025	(a)1 [kg]
5.2	50.96	132.496	(a)1 [kg]
5.25	51.45	135.05625	(a)1 [kg]
5.3	51.94	137.641	(a)1 [kg]
5.35	52.43	140.25025	(a)1 [kg]
5.4	52.92	142.884	(a)1 [kg]
5.45	53.41	145.54225	(a)1 [kg]
5.5	53.9	148.225	(a)1 [kg]
5.55	54.39	150.93225	(a)1 [kg]
5.6	54.88	153.664	(a)1 [kg]
5.65	55.37	156.42025	(a)1 [kg]
5.7	55.86	159.201	(a)1 [kg]
5.75	56.35	162.00625	(a)1 [kg]
5.8	56.84	164.836	(a)1 [kg]
5.85	57.33	167.69025	(a)1 [kg]
5.9	57.82	170.569	(a)1 [kg]
5.95	58.31	173.47225	(a)1 [kg]
6	58.8	176.4	(a)1 [kg]
6.05	59.29	179.35225	(a)1 [kg]
6.1	59.78	182.329	(a)1 [kg]
6.15	60.27	185.33025	(a)1 [kg]
6.2	60.76	188.356	(a)1 [kg]
6.25	61.25	191.40625	(a)1 [kg]
6.3	61.74	194.481	(a)1 [kg]
6.35	62.23	197.58025	(a)1 [kg]
6.4	62.72	200.704	(a)1 [kg]
6.45	63.21	203.85225	(a)1 [kg]
6.5	63.7	207.025	(a)1 [kg]
6.55	64.19	210.22225	(a)1 [kg]
6.6	64.68	213.444	(a)1 [kg]
6.65	65.17	216.69025	(a)1 [kg]
6.7	65.66	219.961	(a)1 [kg]
6.75	66.15	223.25625	(a)1 [kg]
6.8	66.64	226.576	(a)1 [kg]
6.85	67.13	229.92025	(a)1 [kg]
6.9	67.62	233.289	(a)1 [kg]
6.95	68.11	236.68225	(a)1 [kg]
7	68.6	240.1	(a)1 [kg]
7.05	69.09	243.54225	(a)1 [kg]
7.1	69.58	247.009	(a)1 [kg]
7.15	70.07	250.50025	(a)1 [kg]
7.2	70.56	254.016	(a)1 [kg]
7.25	71.05	257.55625	(a)1 [kg]
7.3	71.54	261.121	(a)1 [kg]
7.35	72.03	264.71025	(a)1 [kg]
7.4	72.52	268.324	(a)1 [kg]
7.45	73.01	271.96225	(a)1 [kg]
7.5	73.5	275.625	(a)1 [kg]
7.55	73.99	279.31225	(a)1 [kg]
7.6	74.48	283.024	(a)1 [kg]
7.65	74.97	286.76025	(a)1 [kg]
7.7	75.46	290.521	(a)1 [kg]
7.75	75.95	294.30625	(a)1 [kg]
7.8	76.44	298.116	(a)1 [kg]
7.85	76.93	301.95025	(a)1 [kg]
7.9	77.42	305.809	(a)1 [kg]
7.95	77.91	309.69225	(a)1 [kg]
8	78.4	313.6	(a)1 [kg]
8.05	78.89	317.53225	(a)1 [kg]
8.1	79.38	321.489	(a)1 [kg]
8.15	79.87	325.47025	(a)1 [kg]
8.2	80.36	329.476	(a)1 [kg]
8.25	80.85	333.50625	(a)1 [kg]
8.3	81.34	337.561	(a)1 [kg]
8.35	81.83	341.64025	(a)1 [kg]
8.4	82.32	345.744	(a)1 [kg]
8.45	82.81	349.87225	(a)1 [kg]
8.5	83.3	354.025	(a)1 [kg]
8.55	83.79	358.20225	(a)1 [kg]
8.6	84.28	362.404	(a)1 [kg]
8.65	84.77	366.63025	(a)1 [kg]
8.7	85.26	370.881	(a)1 [kg]
8.75	85.75	375.15625	(a)1 [kg]
8.8	86.24	379.456	(a)1 [kg]
8.85	86.73	383.78025	(a)1 [kg]
8.9	87.22	388.129	(a)1 [kg]
8.95	87.71	392.50225	(a)1 [kg]
9	88.2	396.9	(a)1 [kg]
9.05	88.69	401.32225	(a)1 [kg]
9.1	89.18	405.769	(a)1 [kg]
9.15	89.67	410.24025	(a)1 [kg]
9.2	90.16	414.736	(a)1 [kg]
9.25	90.65	419.25625	(a)1 [kg]
9.3	91.14	423.801	(a)1 [kg]
9.35	91.63	428.37025	(a)1 [kg]
9.4	92.12	432.964	(a)1 [kg]
9.45	92.61	437.58225	(a)1 [kg]
9.5	93.1	442.225	(a)1 [kg]
9.55	93.59	446.89225	(a)1 [kg]
9.6	94.08	451.584	(a)1 [kg]
9.65	94.57	456.30025	(a)1 [kg]
9.7	95.06	461.041	(a)1 [kg]
9.75	95.55	465.80625	(a)1 [kg]
9.8	96.04	470.596	(a)1 [kg]
9.85	96.53	475.41025	(a)1 [kg]
9.9	97.02	480.249	(a)1 [kg]
9.95	97.51	485.11225	(a)1 [kg]
10	98	490	(a)1 [kg]
0	0	0	(b)5[kg]
0.05	0.49	0.01225	(b)5[kg]
0.1	0.98	0.049	(b)5[kg]
0.15	1.47	0.11025	(b)5[kg]
0.2	1.96	0.196	(b)5[kg]
0.25	2.45	0.30625	(b)5[kg]
0.3	2.94	0.441	(b)5[kg]
0.35	3.43	0.60025	(b)5[kg]
0.4	3.92	0.784	(b)5[kg]
0.45	4.41	0.99225	(b)5[kg]
0.5	4.9	1.225	(b)5[kg]
0.55	5.39	1.48225	(b)5[kg]
0.6	5.88	1.764	(b)5[kg]
0.65	6.37	2.07025	(b)5[kg]
0.7	6.86	2.401	(b)5[kg]
0.75	7.35	2.75625	(b)5[kg]
0.8	7.84	3.136	(b)5[kg]
0.85	8.33	3.54025	(b)5[kg]
0.9	8.82	3.969	(b)5[kg]
0.95	9.31	4.42225	(b)5[kg]
1	9.8	4.9	(b)5[kg]
1.05	10.29	5.40225	(b)5[kg]
1.1	10.78	5.929	(b)5[kg]
1.15	11.27	6.48025	(b)5[kg]
1.2	11.76	7.056	(b)5[kg]
1.25	12.25	7.65625	(b)5[kg]
1.3	12.74	8.281	(b)5[kg]
1.35	13.23	8.93025	(b)5[kg]
1.4	13.72	9.604	(b)5[kg]
1.45	14.21	10.30225	(b)5[kg]
1.5	14.7	11.025	(b)5[kg]
1.55	15.19	11.77225	(b)5[kg]
1.6	15.68	12.544	(b)5[kg]
1.65	16.17	13.34025	(b)5[kg]
1.7	16.66	14.161	(b)5[kg]
1.75	17.15	15.00625	(b)5[kg]
1.8	17.64	15.876	(b)5[kg]
1.85	18.13	16.77025	(b)5[kg]
1.9	18.62	17.689	(b)5[kg]
1.95	19.11	18.63225	(b)5[kg]
2	19.6	19.6	(b)5[kg]
2.05	20.09	20.59225	(b)5[kg]
2.1	20.58	21.609	(b)5[kg]
2.15	21.07	22.65025	(b)5[kg]
2.2	21.56	23.716	(b)5[kg]
2.25	22.05	24.80625	(b)5[kg]
2.3	22.54	25.921	(b)5[kg]
2.35	23.03	27.06025	(b)5[kg]
2.4	23.52	28.224	(b)5[kg]
2.45	24.01	29.41225	(b)5[kg]
2.5	24.5	30.625	(b)5[kg]
2.55	24.99	31.86225	(b)5[kg]
2.6	25.48	33.124	(b)5[kg]
2.65	25.97	34.41025	(b)5[kg]
2.7	26.46	35.721	(b)5[kg]
2.75	26.95	37.05625	(b)5[kg]
2.8	27.44	38.416	(b)5[kg]
2.85	27.93	39.80025	(b)5[kg]
2.9	28.42	41.209	(b)5[kg]
2.95	28.91	42.64225	(b)5[kg]
3	29.4	44.1	(b)5[kg]
3.05	29.89	45.58225	(b)5[kg]
3.1	30.38	47.089	(b)5[kg]
3.15	30.87	48.62025	(b)5[kg]
3.2	31.36	50.176	(b)5[kg]
3.25	31.85	51.75625	(b)5[kg]
3.3	32.34	53.361	(b)5[kg]
3.35	32.83	54.99025	(b)5[kg]
3.4	33.32	56.644	(b)5[kg]
3.45	33.81	58.32225	(b)5[kg]
3.5	34.3	60.025	(b)5[kg]
3.55	34.79	61.75225	(b)5[kg]
3.6	35.28	63.504	(b)5[kg]
3.65	35.77	65.28025	(b)5[kg]
3.7	36.26	67.081	(b)5[kg]
3.75	36.75	68.90625	(b)5[kg]
3.8	37.24	70.756	(b)5[kg]
3.85	37.73	72.63025	(b)5[kg]
3.9	38.22	74.529	(b)5[kg]
3.95	38.71	76.45225	(b)5[kg]
4	39.2	78.4	(b)5[kg]
4.05	39.69	80.37225	(b)5[kg]
4.1	40.18	82.369	(b)5[kg]
4.15	40.67	84.39025	(b)5[kg]
4.2	41.16	86.436	(b)5[kg]
4.25	41.65	88.50625	(b)5[kg]
4.3	42.14	90.601	(b)5[kg]
4.35	42.63	92.72025	(b)5[kg]
4.4	43.12	94.864	(b)5[kg]
4.45	43.61	97.03225	(b)5[kg]
4.5	44.1	99.225	(b)5[kg]
4.55	44.59	101.44225	(b)5[kg]
4.6	45.08	103.684	(b)5[kg]
4.65	45.57	105.95025	(b)5[kg]
4.7	46.06	108.241	(b)5[kg]
4.75	46.55	110.55625	(b)5[kg]
4.8	47.04	112.896	(b)5[kg]
4.85	47.53	115.26025	(b)5[kg]
4.9	48.02	117.649	(b)5[kg]
4.95	48.51	120.06225	(b)5[kg]
5	49	122.5	(b)5[kg]
5.05	49.49	124.96225	(b)5[kg]
5.1	49.98	127.449	(b)5[kg]
5.15	50.47	129.96025	(b)5[kg]
5.2	50.96	132.496	(b)5[kg]
5.25	51.45	135.05625	(b)5[kg]
5.3	51.94	137.641	(b)5[kg]
5.35	52.43	140.25025	(b)5[kg]
5.4	52.92	142.884	(b)5[kg]
5.45	53.41	145.54225	(b)5[kg]
5.5	53.9	148.225	(b)5[kg]
5.55	54.39	150.93225	(b)5[kg]
5.6	54.88	153.664	(b)5[kg]
5.65	55.37	156.42025	(b)5[kg]
5.7	55.86	159.201	(b)5[kg]
5.75	56.35	162.00625	(b)5[kg]
5.8	56.84	164.836	(b)5[kg]
5.85	57.33	167.69025	(b)5[kg]
5.9	57.82	170.569	(b)5[kg]
5.95	58.31	173.47225	(b)5[kg]
6	58.8	176.4	(b)5[kg]
6.05	59.29	179.35225	(b)5[kg]
6.1	59.78	182.329	(b)5[kg]
6.15	60.27	185.33025	(b)5[kg]
6.2	60.76	188.356	(b)5[kg]
6.25	61.25	191.40625	(b)5[kg]
6.3	61.74	194.481	(b)5[kg]
6.35	62.23	197.58025	(b)5[kg]
6.4	62.72	200.704	(b)5[kg]
6.45	63.21	203.85225	(b)5[kg]
6.5	63.7	207.025	(b)5[kg]
6.55	64.19	210.22225	(b)5[kg]
6.6	64.68	213.444	(b)5[kg]
6.65	65.17	216.69025	(b)5[kg]
6.7	65.66	219.961	(b)5[kg]
6.75	66.15	223.25625	(b)5[kg]
6.8	66.64	226.576	(b)5[kg]
6.85	67.13	229.92025	(b)5[kg]
6.9	67.62	233.289	(b)5[kg]
6.95	68.11	236.68225	(b)5[kg]
7	68.6	240.1	(b)5[kg]
7.05	69.09	243.54225	(b)5[kg]
7.1	69.58	247.009	(b)5[kg]
7.15	70.07	250.50025	(b)5[kg]
7.2	70.56	254.016	(b)5[kg]
7.25	71.05	257.55625	(b)5[kg]
7.3	71.54	261.121	(b)5[kg]
7.35	72.03	264.71025	(b)5[kg]
7.4	72.52	268.324	(b)5[kg]
7.45	73.01	271.96225	(b)5[kg]
7.5	73.5	275.625	(b)5[kg]
7.55	73.99	279.31225	(b)5[kg]
7.6	74.48	283.024	(b)5[kg]
7.65	74.97	286.76025	(b)5[kg]
7.7	75.46	290.521	(b)5[kg]
7.75	75.95	294.30625	(b)5[kg]
7.8	76.44	298.116	(b)5[kg]
7.85	76.93	301.95025	(b)5[kg]
7.9	77.42	305.809	(b)5[kg]
7.95	77.91	309.69225	(b)5[kg]
8	78.4	313.6	(b)5[kg]
8.05	78.89	317.53225	(b)5[kg]
8.1	79.38	321.489	(b)5[kg]
8.15	79.87	325.47025	(b)5[kg]
8.2	80.36	329.476	(b)5[kg]
8.25	80.85	333.50625	(b)5[kg]
8.3	81.34	337.561	(b)5[kg]
8.35	81.83	341.64025	(b)5[kg]
8.4	82.32	345.744	(b)5[kg]
8.45	82.81	349.87225	(b)5[kg]
8.5	83.3	354.025	(b)5[kg]
8.55	83.79	358.20225	(b)5[kg]
8.6	84.28	362.404	(b)5[kg]
8.65	84.77	366.63025	(b)5[kg]
8.7	85.26	370.881	(b)5[kg]
8.75	85.75	375.15625	(b)5[kg]
8.8	86.24	379.456	(b)5[kg]
8.85	86.73	383.78025	(b)5[kg]
8.9	87.22	388.129	(b)5[kg]
8.95	87.71	392.50225	(b)5[kg]
9	88.2	396.9	(b)5[kg]
9.05	88.69	401.32225	(b)5[kg]
9.1	89.18	405.769	(b)5[kg]
9.15	89.67	410.24025	(b)5[kg]
9.2	90.16	414.736	(b)5[kg]
9.25	90.65	419.25625	(b)5[kg]
9.3	91.14	423.801	(b)5[kg]
9.35	91.63	428.37025	(b)5[kg]
9.4	92.12	432.964	(b)5[kg]
9.45	92.61	437.58225	(b)5[kg]
9.5	93.1	442.225	(b)5[kg]
9.55	93.59	446.89225	(b)5[kg]
9.6	94.08	451.584	(b)5[kg]
9.65	94.57	456.30025	(b)5[kg]
9.7	95.06	461.041	(b)5[kg]
9.75	95.55	465.80625	(b)5[kg]
9.8	96.04	470.596	(b)5[kg]
9.85	96.53	475.41025	(b)5[kg]
9.9	97.02	480.249	(b)5[kg]
9.95	97.51	485.11225	(b)5[kg]
10	98	490	(b)5[kg]
0	0	0	(c)10 [kg]
0.05	0.49	0.01225	(c)10 [kg]
0.1	0.98	0.049	(c)10 [kg]
0.15	1.47	0.11025	(c)10 [kg]
0.2	1.96	0.196	(c)10 [kg]
0.25	2.45	0.30625	(c)10 [kg]
0.3	2.94	0.441	(c)10 [kg]
0.35	3.43	0.60025	(c)10 [kg]
0.4	3.92	0.784	(c)10 [kg]
0.45	4.41	0.99225	(c)10 [kg]
0.5	4.9	1.225	(c)10 [kg]
0.55	5.39	1.48225	(c)10 [kg]
0.6	5.88	1.764	(c)10 [kg]
0.65	6.37	2.07025	(c)10 [kg]
0.7	6.86	2.401	(c)10 [kg]
0.75	7.35	2.75625	(c)10 [kg]
0.8	7.84	3.136	(c)10 [kg]
0.85	8.33	3.54025	(c)10 [kg]
0.9	8.82	3.969	(c)10 [kg]
0.95	9.31	4.42225	(c)10 [kg]
1	9.8	4.9	(c)10 [kg]
1.05	10.29	5.40225	(c)10 [kg]
1.1	10.78	5.929	(c)10 [kg]
1.15	11.27	6.48025	(c)10 [kg]
1.2	11.76	7.056	(c)10 [kg]
1.25	12.25	7.65625	(c)10 [kg]
1.3	12.74	8.281	(c)10 [kg]
1.35	13.23	8.93025	(c)10 [kg]
1.4	13.72	9.604	(c)10 [kg]
1.45	14.21	10.30225	(c)10 [kg]
1.5	14.7	11.025	(c)10 [kg]
1.55	15.19	11.77225	(c)10 [kg]
1.6	15.68	12.544	(c)10 [kg]
1.65	16.17	13.34025	(c)10 [kg]
1.7	16.66	14.161	(c)10 [kg]
1.75	17.15	15.00625	(c)10 [kg]
1.8	17.64	15.876	(c)10 [kg]
1.85	18.13	16.77025	(c)10 [kg]
1.9	18.62	17.689	(c)10 [kg]
1.95	19.11	18.63225	(c)10 [kg]
2	19.6	19.6	(c)10 [kg]
2.05	20.09	20.59225	(c)10 [kg]
2.1	20.58	21.609	(c)10 [kg]
2.15	21.07	22.65025	(c)10 [kg]
2.2	21.56	23.716	(c)10 [kg]
2.25	22.05	24.80625	(c)10 [kg]
2.3	22.54	25.921	(c)10 [kg]
2.35	23.03	27.06025	(c)10 [kg]
2.4	23.52	28.224	(c)10 [kg]
2.45	24.01	29.41225	(c)10 [kg]
2.5	24.5	30.625	(c)10 [kg]
2.55	24.99	31.86225	(c)10 [kg]
2.6	25.48	33.124	(c)10 [kg]
2.65	25.97	34.41025	(c)10 [kg]
2.7	26.46	35.721	(c)10 [kg]
2.75	26.95	37.05625	(c)10 [kg]
2.8	27.44	38.416	(c)10 [kg]
2.85	27.93	39.80025	(c)10 [kg]
2.9	28.42	41.209	(c)10 [kg]
2.95	28.91	42.64225	(c)10 [kg]
3	29.4	44.1	(c)10 [kg]
3.05	29.89	45.58225	(c)10 [kg]
3.1	30.38	47.089	(c)10 [kg]
3.15	30.87	48.62025	(c)10 [kg]
3.2	31.36	50.176	(c)10 [kg]
3.25	31.85	51.75625	(c)10 [kg]
3.3	32.34	53.361	(c)10 [kg]
3.35	32.83	54.99025	(c)10 [kg]
3.4	33.32	56.644	(c)10 [kg]
3.45	33.81	58.32225	(c)10 [kg]
3.5	34.3	60.025	(c)10 [kg]
3.55	34.79	61.75225	(c)10 [kg]
3.6	35.28	63.504	(c)10 [kg]
3.65	35.77	65.28025	(c)10 [kg]
3.7	36.26	67.081	(c)10 [kg]
3.75	36.75	68.90625	(c)10 [kg]
3.8	37.24	70.756	(c)10 [kg]
3.85	37.73	72.63025	(c)10 [kg]
3.9	38.22	74.529	(c)10 [kg]
3.95	38.71	76.45225	(c)10 [kg]
4	39.2	78.4	(c)10 [kg]
4.05	39.69	80.37225	(c)10 [kg]
4.1	40.18	82.369	(c)10 [kg]
4.15	40.67	84.39025	(c)10 [kg]
4.2	41.16	86.436	(c)10 [kg]
4.25	41.65	88.50625	(c)10 [kg]
4.3	42.14	90.601	(c)10 [kg]
4.35	42.63	92.72025	(c)10 [kg]
4.4	43.12	94.864	(c)10 [kg]
4.45	43.61	97.03225	(c)10 [kg]
4.5	44.1	99.225	(c)10 [kg]
4.55	44.59	101.44225	(c)10 [kg]
4.6	45.08	103.684	(c)10 [kg]
4.65	45.57	105.95025	(c)10 [kg]
4.7	46.06	108.241	(c)10 [kg]
4.75	46.55	110.55625	(c)10 [kg]
4.8	47.04	112.896	(c)10 [kg]
4.85	47.53	115.26025	(c)10 [kg]
4.9	48.02	117.649	(c)10 [kg]
4.95	48.51	120.06225	(c)10 [kg]
5	49	122.5	(c)10 [kg]
5.05	49.49	124.96225	(c)10 [kg]
5.1	49.98	127.449	(c)10 [kg]
5.15	50.47	129.96025	(c)10 [kg]
5.2	50.96	132.496	(c)10 [kg]
5.25	51.45	135.05625	(c)10 [kg]
5.3	51.94	137.641	(c)10 [kg]
5.35	52.43	140.25025	(c)10 [kg]
5.4	52.92	142.884	(c)10 [kg]
5.45	53.41	145.54225	(c)10 [kg]
5.5	53.9	148.225	(c)10 [kg]
5.55	54.39	150.93225	(c)10 [kg]
5.6	54.88	153.664	(c)10 [kg]
5.65	55.37	156.42025	(c)10 [kg]
5.7	55.86	159.201	(c)10 [kg]
5.75	56.35	162.00625	(c)10 [kg]
5.8	56.84	164.836	(c)10 [kg]
5.85	57.33	167.69025	(c)10 [kg]
5.9	57.82	170.569	(c)10 [kg]
5.95	58.31	173.47225	(c)10 [kg]
6	58.8	176.4	(c)10 [kg]
6.05	59.29	179.35225	(c)10 [kg]
6.1	59.78	182.329	(c)10 [kg]
6.15	60.27	185.33025	(c)10 [kg]
6.2	60.76	188.356	(c)10 [kg]
6.25	61.25	191.40625	(c)10 [kg]
6.3	61.74	194.481	(c)10 [kg]
6.35	62.23	197.58025	(c)10 [kg]
6.4	62.72	200.704	(c)10 [kg]
6.45	63.21	203.85225	(c)10 [kg]
6.5	63.7	207.025	(c)10 [kg]
6.55	64.19	210.22225	(c)10 [kg]
6.6	64.68	213.444	(c)10 [kg]
6.65	65.17	216.69025	(c)10 [kg]
6.7	65.66	219.961	(c)10 [kg]
6.75	66.15	223.25625	(c)10 [kg]
6.8	66.64	226.576	(c)10 [kg]
6.85	67.13	229.92025	(c)10 [kg]
6.9	67.62	233.289	(c)10 [kg]
6.95	68.11	236.68225	(c)10 [kg]
7	68.6	240.1	(c)10 [kg]
7.05	69.09	243.54225	(c)10 [kg]
7.1	69.58	247.009	(c)10 [kg]
7.15	70.07	250.50025	(c)10 [kg]
7.2	70.56	254.016	(c)10 [kg]
7.25	71.05	257.55625	(c)10 [kg]
7.3	71.54	261.121	(c)10 [kg]
7.35	72.03	264.71025	(c)10 [kg]
7.4	72.52	268.324	(c)10 [kg]
7.45	73.01	271.96225	(c)10 [kg]
7.5	73.5	275.625	(c)10 [kg]
7.55	73.99	279.31225	(c)10 [kg]
7.6	74.48	283.024	(c)10 [kg]
7.65	74.97	286.76025	(c)10 [kg]
7.7	75.46	290.521	(c)10 [kg]
7.75	75.95	294.30625	(c)10 [kg]
7.8	76.44	298.116	(c)10 [kg]
7.85	76.93	301.95025	(c)10 [kg]
7.9	77.42	305.809	(c)10 [kg]
7.95	77.91	309.69225	(c)10 [kg]
8	78.4	313.6	(c)10 [kg]
8.05	78.89	317.53225	(c)10 [kg]
8.1	79.38	321.489	(c)10 [kg]
8.15	79.87	325.47025	(c)10 [kg]
8.2	80.36	329.476	(c)10 [kg]
8.25	80.85	333.50625	(c)10 [kg]
8.3	81.34	337.561	(c)10 [kg]
8.35	81.83	341.64025	(c)10 [kg]
8.4	82.32	345.744	(c)10 [kg]
8.45	82.81	349.87225	(c)10 [kg]
8.5	83.3	354.025	(c)10 [kg]
8.55	83.79	358.20225	(c)10 [kg]
8.6	84.28	362.404	(c)10 [kg]
8.65	84.77	366.63025	(c)10 [kg]
8.7	85.26	370.881	(c)10 [kg]
8.75	85.75	375.15625	(c)10 [kg]
8.8	86.24	379.456	(c)10 [kg]
8.85	86.73	383.78025	(c)10 [kg]
8.9	87.22	388.129	(c)10 [kg]
8.95	87.71	392.50225	(c)10 [kg]
9	88.2	396.9	(c)10 [kg]
9.05	88.69	401.32225	(c)10 [kg]
9.1	89.18	405.769	(c)10 [kg]
9.15	89.67	410.24025	(c)10 [kg]
9.2	90.16	414.736	(c)10 [kg]
9.25	90.65	419.25625	(c)10 [kg]
9.3	91.14	423.801	(c)10 [kg]
9.35	91.63	428.37025	(c)10 [kg]
9.4	92.12	432.964	(c)10 [kg]
9.45	92.61	437.58225	(c)10 [kg]
9.5	93.1	442.225	(c)10 [kg]
9.55	93.59	446.89225	(c)10 [kg]
9.6	94.08	451.584	(c)10 [kg]
9.65	94.57	456.30025	(c)10 [kg]
9.7	95.06	461.041	(c)10 [kg]
9.75	95.55	465.80625	(c)10 [kg]
9.8	96.04	470.596	(c)10 [kg]
9.85	96.53	475.41025	(c)10 [kg]
9.9	97.02	480.249	(c)10 [kg]
9.95	97.51	485.11225	(c)10 [kg]
10	98	490	(c)10 [kg]

この CSV を桜チャートに貼り付け、X 軸を t[s]、Y 軸を v[m/s]、LEVEL を LEVEL[kg] にすると、 1kg・5kg・10kg の 3 本が完全に重なって 1 本の直線として表示されます。

4-2. 空気抵抗あり（質量によってカーブが分かれるデータ）

こちらは空気抵抗あり（1kg, 5kg, 10kg）のサンプルデータです。同様に、ボタンを押すとフルデータがコピーされます。

t[s]	v[m/s]	x[m]	LEVEL[kg]
0	0	0	(a)1[kg]
0.05	0.47795	0.0239	(a)1[kg]
0.1	0.93259	0.07053	(a)1[kg]
0.15	1.36506	0.13878	(a)1[kg]
0.2	1.77644	0.2276	(a)1[kg]
0.25	2.16775	0.33599	(a)1[kg]
0.3	2.53998	0.46299	(a)1[kg]
0.35	2.89406	0.60769	(a)1[kg]
0.4	3.23086	0.76923	(a)1[kg]
0.45	3.55124	0.9468	(a)1[kg]
0.5	3.856	1.1396	(a)1[kg]
0.55	4.14589	1.34689	(a)1[kg]
0.6	4.42165	1.56797	(a)1[kg]
0.65	4.68395	1.80217	(a)1[kg]
0.7	4.93346	2.04884	(a)1[kg]
0.75	5.17081	2.30739	(a)1[kg]
0.8	5.39658	2.57721	(a)1[kg]
0.85	5.61133	2.85778	(a)1[kg]
0.9	5.81562	3.14856	(a)1[kg]
0.95	6.00994	3.44906	(a)1[kg]
1	6.19478	3.7588	(a)1[kg]
1.05	6.37061	4.07733	(a)1[kg]
1.1	6.53786	4.40422	(a)1[kg]
1.15	6.69696	4.73907	(a)1[kg]
1.2	6.8483	5.08148	(a)1[kg]
1.25	6.99225	5.4311	(a)1[kg]
1.3	7.12919	5.78756	(a)1[kg]
1.35	7.25945	6.15053	(a)1[kg]
1.4	7.38335	6.5197	(a)1[kg]
1.45	7.50121	6.89476	(a)1[kg]
1.5	7.61332	7.27542	(a)1[kg]
1.55	7.71997	7.66142	(a)1[kg]
1.6	7.82141	8.05249	(a)1[kg]
1.65	7.91791	8.44839	(a)1[kg]
1.7	8.0097	8.84887	(a)1[kg]
1.75	8.09702	9.25372	(a)1[kg]
1.8	8.18007	9.66273	(a)1[kg]
1.85	8.25908	10.07568	(a)1[kg]
1.9	8.33423	10.49239	(a)1[kg]
1.95	8.40571	10.91268	(a)1[kg]
2	8.47371	11.33636	(a)1[kg]
2.05	8.5384	11.76328	(a)1[kg]
2.1	8.59993	12.19328	(a)1[kg]
2.15	8.65846	12.6262	(a)1[kg]
2.2	8.71413	13.06191	(a)1[kg]
2.25	8.76709	13.50026	(a)1[kg]
2.3	8.81746	13.94114	(a)1[kg]
2.35	8.86538	14.38441	(a)1[kg]
2.4	8.91096	14.82995	(a)1[kg]
2.45	8.95432	15.27767	(a)1[kg]
2.5	8.99557	15.72745	(a)1[kg]
2.55	9.0348	16.17919	(a)1[kg]
2.6	9.07212	16.63279	(a)1[kg]
2.65	9.10762	17.08818	(a)1[kg]
2.7	9.14139	17.54524	(a)1[kg]
2.75	9.17351	18.00392	(a)1[kg]
2.8	9.20406	18.46412	(a)1[kg]
2.85	9.23313	18.92578	(a)1[kg]
2.9	9.26077	19.38882	(a)1[kg]
2.95	9.28707	19.85317	(a)1[kg]
3	9.31209	20.31878	(a)1[kg]
3.05	9.33588	20.78557	(a)1[kg]
3.1	9.35852	21.2535	(a)1[kg]
3.15	9.38005	21.7225	(a)1[kg]
3.2	9.40053	22.19252	(a)1[kg]
3.25	9.42001	22.66353	(a)1[kg]
3.3	9.43854	23.13545	(a)1[kg]
3.35	9.45617	23.60826	(a)1[kg]
3.4	9.47294	24.08191	(a)1[kg]
3.45	9.48889	24.55635	(a)1[kg]
3.5	9.50407	25.03156	(a)1[kg]
3.55	9.5185	25.50748	(a)1[kg]
3.6	9.53223	25.98409	(a)1[kg]
3.65	9.54529	26.46136	(a)1[kg]
3.7	9.55771	26.93924	(a)1[kg]
3.75	9.56953	27.41772	(a)1[kg]
3.8	9.58077	27.89676	(a)1[kg]
3.85	9.59146	28.37633	(a)1[kg]
3.9	9.60163	28.85641	(a)1[kg]
3.95	9.6113	29.33698	(a)1[kg]
4	9.62051	29.818	(a)1[kg]
4.05	9.62926	30.29946	(a)1[kg]
4.1	9.63759	30.78134	(a)1[kg]
4.15	9.64551	31.26362	(a)1[kg]
4.2	9.65304	31.74627	(a)1[kg]
4.25	9.66021	32.22928	(a)1[kg]
4.3	9.66703	32.71263	(a)1[kg]
4.35	9.67351	33.19631	(a)1[kg]
4.4	9.67968	33.68029	(a)1[kg]
4.45	9.68555	34.16457	(a)1[kg]
4.5	9.69113	34.64913	(a)1[kg]
4.55	9.69644	35.13395	(a)1[kg]
4.6	9.70149	35.61902	(a)1[kg]
4.65	9.7063	36.10434	(a)1[kg]
4.7	9.71087	36.58988	(a)1[kg]
4.75	9.71521	37.07564	(a)1[kg]
4.8	9.71935	37.56161	(a)1[kg]
4.85	9.72328	38.04777	(a)1[kg]
4.9	9.72702	38.53413	(a)1[kg]
4.95	9.73058	39.02065	(a)1[kg]
5	9.73397	39.50735	(a)1[kg]
5.05	9.73719	39.99421	(a)1[kg]
5.1	9.74025	40.48123	(a)1[kg]
5.15	9.74317	40.96838	(a)1[kg]
5.2	9.74594	41.45568	(a)1[kg]
5.25	9.74857	41.94311	(a)1[kg]
5.3	9.75108	42.43066	(a)1[kg]
5.35	9.75347	42.91834	(a)1[kg]
5.4	9.75574	43.40612	(a)1[kg]
5.45	9.7579	43.89402	(a)1[kg]
5.5	9.75995	44.38202	(a)1[kg]
5.55	9.7619	44.87011	(a)1[kg]
5.6	9.76376	45.3583	(a)1[kg]
5.65	9.76553	45.84658	(a)1[kg]
5.7	9.76721	46.33494	(a)1[kg]
5.75	9.76881	46.82338	(a)1[kg]
5.8	9.77033	47.31189	(a)1[kg]
5.85	9.77178	47.80048	(a)1[kg]
5.9	9.77315	48.28914	(a)1[kg]
5.95	9.77446	48.77786	(a)1[kg]
6	9.77571	49.26665	(a)1[kg]
6.05	9.77689	49.75549	(a)1[kg]
6.1	9.77802	50.24439	(a)1[kg]
6.15	9.77909	50.73335	(a)1[kg]
6.2	9.78011	51.22235	(a)1[kg]
6.25	9.78108	51.71141	(a)1[kg]
6.3	9.782	52.20051	(a)1[kg]
6.35	9.78288	52.68965	(a)1[kg]
6.4	9.78372	53.17884	(a)1[kg]
6.45	9.78451	53.66806	(a)1[kg]
6.5	9.78527	54.15733	(a)1[kg]
6.55	9.78598	54.64663	(a)1[kg]
6.6	9.78667	55.13596	(a)1[kg]
6.65	9.78732	55.62533	(a)1[kg]
6.7	9.78794	56.11472	(a)1[kg]
6.75	9.78853	56.60415	(a)1[kg]
6.8	9.78909	57.0936	(a)1[kg]
6.85	9.78962	57.58308	(a)1[kg]
6.9	9.79012	58.07259	(a)1[kg]
6.95	9.79061	58.56212	(a)1[kg]
7	9.79106	59.05167	(a)1[kg]
7.05	9.7915	59.54125	(a)1[kg]
7.1	9.79191	60.03084	(a)1[kg]
7.15	9.79231	60.52046	(a)1[kg]
7.2	9.79268	61.01009	(a)1[kg]
7.25	9.79304	61.49975	(a)1[kg]
7.3	9.79338	61.98941	(a)1[kg]
7.35	9.7937	62.4791	(a)1[kg]
7.4	9.79401	62.9688	(a)1[kg]
7.45	9.7943	63.45852	(a)1[kg]
7.5	9.79458	63.94824	(a)1[kg]
7.55	9.79484	64.43799	(a)1[kg]
7.6	9.7951	64.92774	(a)1[kg]
7.65	9.79533	65.41751	(a)1[kg]
7.7	9.79556	65.90729	(a)1[kg]
7.75	9.79578	66.39708	(a)1[kg]
7.8	9.79598	66.88687	(a)1[kg]
7.85	9.79618	67.37668	(a)1[kg]
7.9	9.79637	67.8665	(a)1[kg]
7.95	9.79654	68.35633	(a)1[kg]
8	9.79671	68.84616	(a)1[kg]
8.05	9.79687	69.33601	(a)1[kg]
8.1	9.79703	69.82586	(a)1[kg]
8.15	9.79717	70.31572	(a)1[kg]
8.2	9.79731	70.80558	(a)1[kg]
8.25	9.79744	71.29546	(a)1[kg]
8.3	9.79756	71.78533	(a)1[kg]
8.35	9.79768	72.27522	(a)1[kg]
8.4	9.7978	72.76511	(a)1[kg]
8.45	9.7979	73.255	(a)1[kg]
8.5	9.79801	73.7449	(a)1[kg]
8.55	9.7981	74.23481	(a)1[kg]
8.6	9.7982	74.72472	(a)1[kg]
8.65	9.79828	75.21463	(a)1[kg]
8.7	9.79837	75.70455	(a)1[kg]
8.75	9.79845	76.19447	(a)1[kg]
8.8	9.79852	76.6844	(a)1[kg]
8.85	9.79859	77.17433	(a)1[kg]
8.9	9.79866	77.66426	(a)1[kg]
8.95	9.79873	78.1542	(a)1[kg]
9	9.79879	78.64414	(a)1[kg]
9.05	9.79885	79.13408	(a)1[kg]
9.1	9.79891	79.62403	(a)1[kg]
9.15	9.79896	80.11397	(a)1[kg]
9.2	9.79901	80.60392	(a)1[kg]
9.25	9.79906	81.09388	(a)1[kg]
9.3	9.7991	81.58383	(a)1[kg]
9.35	9.79915	82.07379	(a)1[kg]
9.4	9.79919	82.56375	(a)1[kg]
9.45	9.79923	83.05371	(a)1[kg]
9.5	9.79927	83.54367	(a)1[kg]
9.55	9.7993	84.03364	(a)1[kg]
9.6	9.79934	84.52361	(a)1[kg]
9.65	9.79937	85.01357	(a)1[kg]
9.7	9.7994	85.50354	(a)1[kg]
9.75	9.79943	85.99352	(a)1[kg]
9.8	9.79946	86.48349	(a)1[kg]
9.85	9.79948	86.97346	(a)1[kg]
9.9	9.79951	87.46344	(a)1[kg]
9.95	9.79953	87.95341	(a)1[kg]
10	9.79956	88.44339	(a)1[kg]
0	0	0	(b)5[kg]
0.05	0.48756	0.02438	(b)5[kg]
0.1	0.97027	0.07289	(b)5[kg]
0.15	1.44817	0.1453	(b)5[kg]
0.2	1.92132	0.24137	(b)5[kg]
0.25	2.38976	0.36085	(b)5[kg]
0.3	2.85354	0.50353	(b)5[kg]
0.35	3.3127	0.66917	(b)5[kg]
0.4	3.7673	0.85753	(b)5[kg]
0.45	4.21737	1.0684	(b)5[kg]
0.5	4.66297	1.30155	(b)5[kg]
0.55	5.10413	1.55675	(b)5[kg]
0.6	5.5409	1.8338	(b)5[kg]
0.65	5.97332	2.13246	(b)5[kg]
0.7	6.40145	2.45254	(b)5[kg]
0.75	6.82531	2.7938	(b)5[kg]
0.8	7.24495	3.15605	(b)5[kg]
0.85	7.66042	3.53907	(b)5[kg]
0.9	8.07176	3.94266	(b)5[kg]
0.95	8.479	4.36661	(b)5[kg]
1	8.88219	4.81072	(b)5[kg]
1.05	9.28137	5.27479	(b)5[kg]
1.1	9.67658	5.75862	(b)5[kg]
1.15	10.06785	6.26201	(b)5[kg]
1.2	10.45523	6.78477	(b)5[kg]
1.25	10.83876	7.32671	(b)5[kg]
1.3	11.21847	7.88763	(b)5[kg]
1.35	11.5944	8.46735	(b)5[kg]
1.4	11.9666	9.06568	(b)5[kg]
1.45	12.33509	9.68244	(b)5[kg]
1.5	12.69991	10.31743	(b)5[kg]
1.55	13.0611	10.97049	(b)5[kg]
1.6	13.4187	11.64142	(b)5[kg]
1.65	13.77274	12.33006	(b)5[kg]
1.7	14.12325	13.03622	(b)5[kg]
1.75	14.47028	13.75974	(b)5[kg]
1.8	14.81386	14.50043	(b)5[kg]
1.85	15.15402	15.25813	(b)5[kg]
1.9	15.49079	16.03267	(b)5[kg]
1.95	15.82421	16.82388	(b)5[kg]
2	16.15432	17.6316	(b)5[kg]
2.05	16.48114	18.45565	(b)5[kg]
2.1	16.80471	19.29589	(b)5[kg]
2.15	17.12505	20.15214	(b)5[kg]
2.2	17.44222	21.02425	(b)5[kg]
2.25	17.75622	21.91206	(b)5[kg]
2.3	18.0671	22.81542	(b)5[kg]
2.35	18.37489	23.73416	(b)5[kg]
2.4	18.67961	24.66814	(b)5[kg]
2.45	18.98131	25.61721	(b)5[kg]
2.5	19.28	26.58121	(b)5[kg]
2.55	19.57572	27.55999	(b)5[kg]
2.6	19.86849	28.55342	(b)5[kg]
2.65	20.15836	29.56134	(b)5[kg]
2.7	20.44534	30.5836	(b)5[kg]
2.75	20.72946	31.62008	(b)5[kg]
2.8	21.01076	32.67061	(b)5[kg]
2.85	21.28925	33.73508	(b)5[kg]
2.9	21.56498	34.81333	(b)5[kg]
2.95	21.83796	35.90522	(b)5[kg]
3	22.10823	37.01064	(b)5[kg]
3.05	22.37581	38.12943	(b)5[kg]
3.1	22.64072	39.26146	(b)5[kg]
3.15	22.903	40.40661	(b)5[kg]
3.2	23.16267	41.56475	(b)5[kg]
3.25	23.41976	42.73573	(b)5[kg]
3.3	23.67428	43.91945	(b)5[kg]
3.35	23.92628	45.11576	(b)5[kg]
3.4	24.17577	46.32455	(b)5[kg]
3.45	24.42277	47.54569	(b)5[kg]
3.5	24.66732	48.77905	(b)5[kg]
3.55	24.90943	50.02453	(b)5[kg]
3.6	25.14914	51.28198	(b)5[kg]
3.65	25.38646	52.55131	(b)5[kg]
3.7	25.62142	53.83238	(b)5[kg]
3.75	25.85404	55.12508	(b)5[kg]
3.8	26.08435	56.4293	(b)5[kg]
3.85	26.31236	57.74491	(b)5[kg]
3.9	26.53811	59.07182	(b)5[kg]
3.95	26.76161	60.4099	(b)5[kg]
4	26.98288	61.75904	(b)5[kg]
4.05	27.20195	63.11914	(b)5[kg]
4.1	27.41885	64.49008	(b)5[kg]
4.15	27.63359	65.87176	(b)5[kg]
4.2	27.84618	67.26407	(b)5[kg]
4.25	28.05667	68.66691	(b)5[kg]
4.3	28.26506	70.08016	(b)5[kg]
4.35	28.47137	71.50373	(b)5[kg]
4.4	28.67564	72.93751	(b)5[kg]
4.45	28.87787	74.3814	(b)5[kg]
4.5	29.07809	75.83531	(b)5[kg]
4.55	29.27631	77.29912	(b)5[kg]
4.6	29.47257	78.77275	(b)5[kg]
4.65	29.66687	80.25609	(b)5[kg]
4.7	29.85924	81.74906	(b)5[kg]
4.75	30.04969	83.25154	(b)5[kg]
4.8	30.23825	84.76345	(b)5[kg]
4.85	30.42493	86.2847	(b)5[kg]
4.9	30.60976	87.81519	(b)5[kg]
4.95	30.79274	89.35482	(b)5[kg]
5	30.97391	90.90352	(b)5[kg]
5.05	31.15327	92.46118	(b)5[kg]
5.1	31.33085	94.02773	(b)5[kg]
5.15	31.50666	95.60306	(b)5[kg]
5.2	31.68072	97.1871	(b)5[kg]
5.25	31.85305	98.77975	(b)5[kg]
5.3	32.02367	100.38093	(b)5[kg]
5.35	32.19258	101.99056	(b)5[kg]
5.4	32.35982	103.60855	(b)5[kg]
5.45	32.52539	105.23482	(b)5[kg]
5.5	32.68932	106.86929	(b)5[kg]
5.55	32.85161	108.51187	(b)5[kg]
5.6	33.01229	110.16248	(b)5[kg]
5.65	33.17137	111.82105	(b)5[kg]
5.7	33.32887	113.48749	(b)5[kg]
5.75	33.4848	115.16173	(b)5[kg]
5.8	33.63918	116.84369	(b)5[kg]
5.85	33.79202	118.53329	(b)5[kg]
5.9	33.94334	120.23046	(b)5[kg]
5.95	34.09316	121.93512	(b)5[kg]
6	34.24148	123.64719	(b)5[kg]
6.05	34.38833	125.36661	(b)5[kg]
6.1	34.53372	127.0933	(b)5[kg]
6.15	34.67766	128.82718	(b)5[kg]
6.2	34.82017	130.56819	(b)5[kg]
6.25	34.96126	132.31625	(b)5[kg]
6.3	35.10095	134.0713	(b)5[kg]
6.35	35.23925	135.83326	(b)5[kg]
6.4	35.37617	137.60207	(b)5[kg]
6.45	35.51173	139.37766	(b)5[kg]
6.5	35.64594	141.15995	(b)5[kg]
6.55	35.77882	142.94889	(b)5[kg]
6.6	35.91037	144.74441	(b)5[kg]
6.65	36.04061	146.54644	(b)5[kg]
6.7	36.16956	148.35492	(b)5[kg]
6.75	36.29723	150.16978	(b)5[kg]
6.8	36.42362	151.99096	(b)5[kg]
6.85	36.54876	153.8184	(b)5[kg]
6.9	36.67265	155.65203	(b)5[kg]
6.95	36.79531	157.4918	(b)5[kg]
7	36.91675	159.33764	(b)5[kg]
7.05	37.03698	161.18949	(b)5[kg]
7.1	37.15601	163.04729	(b)5[kg]
7.15	37.27386	164.91098	(b)5[kg]
7.2	37.39054	166.78051	(b)5[kg]
7.25	37.50606	168.65581	(b)5[kg]
7.3	37.62042	170.53683	(b)5[kg]
7.35	37.73365	172.42351	(b)5[kg]
7.4	37.84575	174.3158	(b)5[kg]
7.45	37.95674	176.21364	(b)5[kg]
7.5	38.06662	178.11697	(b)5[kg]
7.55	38.17541	180.02574	(b)5[kg]
7.6	38.28312	181.9399	(b)5[kg]
7.65	38.38975	183.85938	(b)5[kg]
7.7	38.49533	185.78415	(b)5[kg]
7.75	38.59985	187.71414	(b)5[kg]
7.8	38.70333	189.64931	(b)5[kg]
7.85	38.80579	191.5896	(b)5[kg]
7.9	38.90722	193.53496	(b)5[kg]
7.95	39.00764	195.48534	(b)5[kg]
8	39.10707	197.44069	(b)5[kg]
8.05	39.20551	199.40097	(b)5[kg]
8.1	39.30296	201.36612	(b)5[kg]
8.15	39.39945	203.33609	(b)5[kg]
8.2	39.49498	205.31084	(b)5[kg]
8.25	39.58955	207.29032	(b)5[kg]
8.3	39.68319	209.27448	(b)5[kg]
8.35	39.77589	211.26327	(b)5[kg]
8.4	39.86768	213.25665	(b)5[kg]
8.45	39.95854	215.25458	(b)5[kg]
8.5	40.04851	217.25701	(b)5[kg]
8.55	40.13758	219.26389	(b)5[kg]
8.6	40.22576	221.27517	(b)5[kg]
8.65	40.31306	223.29083	(b)5[kg]
8.7	40.3995	225.3108	(b)5[kg]
8.75	40.48508	227.33506	(b)5[kg]
8.8	40.5698	229.36355	(b)5[kg]
8.85	40.65368	231.39623	(b)5[kg]
8.9	40.73673	233.43307	(b)5[kg]
8.95	40.81895	235.47401	(b)5[kg]
9	40.90035	237.51903	(b)5[kg]
9.05	40.98095	239.56808	(b)5[kg]
9.1	41.06074	241.62112	(b)5[kg]
9.15	41.13974	243.6781	(b)5[kg]
9.2	41.21795	245.739	(b)5[kg]
9.25	41.29538	247.80377	(b)5[kg]
9.3	41.37204	249.87237	(b)5[kg]
9.35	41.44794	251.94477	(b)5[kg]
9.4	41.52308	254.02092	(b)5[kg]
9.45	41.59748	256.1008	(b)5[kg]
9.5	41.67114	258.18435	(b)5[kg]
9.55	41.74406	260.27156	(b)5[kg]
9.6	41.81626	262.36237	(b)5[kg]
9.65	41.88774	264.45676	(b)5[kg]
9.7	41.95851	266.55468	(b)5[kg]
9.75	42.02857	268.65611	(b)5[kg]
9.8	42.09794	270.76101	(b)5[kg]
9.85	42.16661	272.86934	(b)5[kg]
9.9	42.23461	274.98107	(b)5[kg]
9.95	42.30192	277.09616	(b)5[kg]
10	42.36857	279.21459	(b)5[kg]
0	0	0	(c)10[kg]
0.05	0.48878	0.02444	(c)10[kg]
0.1	0.97512	0.07319	(c)10[kg]
0.15	1.45903	0.14615	(c)10[kg]
0.2	1.94053	0.24317	(c)10[kg]
0.25	2.41963	0.36415	(c)10[kg]
0.3	2.89634	0.50897	(c)10[kg]
0.35	3.37067	0.6775	(c)10[kg]
0.4	3.84263	0.86964	(c)10[kg]
0.45	4.31225	1.08525	(c)10[kg]
0.5	4.77952	1.32422	(c)10[kg]
0.55	5.24446	1.58645	(c)10[kg]
0.6	5.70708	1.8718	(c)10[kg]
0.65	6.16739	2.18017	(c)10[kg]
0.7	6.62541	2.51144	(c)10[kg]
0.75	7.08114	2.8655	(c)10[kg]
0.8	7.5346	3.24223	(c)10[kg]
0.85	7.9858	3.64152	(c)10[kg]
0.9	8.43474	4.06325	(c)10[kg]
0.95	8.88145	4.50733	(c)10[kg]
1	9.32593	4.97362	(c)10[kg]
1.05	9.7682	5.46203	(c)10[kg]
1.1	10.20825	5.97245	(c)10[kg]
1.15	10.64612	6.50475	(c)10[kg]
1.2	11.0818	7.05884	(c)10[kg]
1.25	11.5153	7.63461	(c)10[kg]
1.3	11.94665	8.23194	(c)10[kg]
1.35	12.37584	8.85073	(c)10[kg]
1.4	12.80289	9.49088	(c)10[kg]
1.45	13.22782	10.15227	(c)10[kg]
1.5	13.65062	10.8348	(c)10[kg]
1.55	14.07131	11.53836	(c)10[kg]
1.6	14.48991	12.26286	(c)10[kg]
1.65	14.90642	13.00818	(c)10[kg]
1.7	15.32085	13.77422	(c)10[kg]
1.75	15.73321	14.56088	(c)10[kg]
1.8	16.14352	15.36806	(c)10[kg]
1.85	16.55178	16.19565	(c)10[kg]
1.9	16.958	17.04355	(c)10[kg]
1.95	17.3622	17.91166	(c)10[kg]
2	17.76439	18.79988	(c)10[kg]
2.05	18.16456	19.70811	(c)10[kg]
2.1	18.56274	20.63624	(c)10[kg]
2.15	18.95894	21.58419	(c)10[kg]
2.2	19.35316	22.55185	(c)10[kg]
2.25	19.74541	23.53912	(c)10[kg]
2.3	20.13571	24.5459	(c)10[kg]
2.35	20.52406	25.57211	(c)10[kg]
2.4	20.91047	26.61763	(c)10[kg]
2.45	21.29496	27.68238	(c)10[kg]
2.5	21.67752	28.76625	(c)10[kg]
2.55	22.05818	29.86916	(c)10[kg]
2.6	22.43694	30.99101	(c)10[kg]
2.65	22.81382	32.1317	(c)10[kg]
2.7	23.18881	33.29114	(c)10[kg]
2.75	23.56193	34.46924	(c)10[kg]
2.8	23.93319	35.6659	(c)10[kg]
2.85	24.3026	36.88103	(c)10[kg]
2.9	24.67017	38.11454	(c)10[kg]
2.95	25.0359	39.36633	(c)10[kg]
3	25.39981	40.63632	(c)10[kg]
3.05	25.76191	41.92442	(c)10[kg]
3.1	26.1222	43.23053	(c)10[kg]
3.15	26.48069	44.55456	(c)10[kg]
3.2	26.83739	45.89643	(c)10[kg]
3.25	27.19232	47.25605	(c)10[kg]
3.3	27.54547	48.63332	(c)10[kg]
3.35	27.89687	50.02817	(c)10[kg]
3.4	28.24651	51.44049	(c)10[kg]
3.45	28.59441	52.87021	(c)10[kg]
3.5	28.94057	54.31724	(c)10[kg]
3.55	29.285	55.78149	(c)10[kg]
3.6	29.62772	57.26288	(c)10[kg]
3.65	29.96873	58.76131	(c)10[kg]
3.7	30.30804	60.27671	(c)10[kg]
3.75	30.64565	61.809	(c)10[kg]
3.8	30.98158	63.35808	(c)10[kg]
3.85	31.31584	64.92387	(c)10[kg]
3.9	31.64843	66.50629	(c)10[kg]
3.95	31.97936	68.10526	(c)10[kg]
4	32.30864	69.72069	(c)10[kg]
4.05	32.63627	71.3525	(c)10[kg]
4.1	32.96228	73.00062	(c)10[kg]
4.15	33.28665	74.66495	(c)10[kg]
4.2	33.60941	76.34542	(c)10[kg]
4.25	33.93056	78.04195	(c)10[kg]
4.3	34.25011	79.75445	(c)10[kg]
4.35	34.56806	81.48286	(c)10[kg]
4.4	34.88443	83.22708	(c)10[kg]
4.45	35.19922	84.98704	(c)10[kg]
4.5	35.51244	86.76266	(c)10[kg]
4.55	35.8241	88.55386	(c)10[kg]
4.6	36.1342	90.36057	(c)10[kg]
4.65	36.44276	92.18271	(c)10[kg]
4.7	36.74978	94.0202	(c)10[kg]
4.75	37.05526	95.87297	(c)10[kg]
4.8	37.35923	97.74093	(c)10[kg]
4.85	37.66167	99.62401	(c)10[kg]
4.9	37.96261	101.52214	(c)10[kg]
4.95	38.26205	103.43524	(c)10[kg]
5	38.56	105.36324	(c)10[kg]
5.05	38.85645	107.30607	(c)10[kg]
5.1	39.15143	109.26364	(c)10[kg]
5.15	39.44494	111.23588	(c)10[kg]
5.2	39.73699	113.22273	(c)10[kg]
5.25	40.02757	115.22411	(c)10[kg]
5.3	40.31671	117.23995	(c)10[kg]
5.35	40.60441	119.27017	(c)10[kg]
5.4	40.89067	121.3147	(c)10[kg]
5.45	41.17551	123.37348	(c)10[kg]
5.5	41.45892	125.44642	(c)10[kg]
5.55	41.74092	127.53347	(c)10[kg]
5.6	42.02151	129.63455	(c)10[kg]
5.65	42.30071	131.74958	(c)10[kg]
5.7	42.57851	133.87851	(c)10[kg]
5.75	42.85492	136.02125	(c)10[kg]
5.8	43.12996	138.17775	(c)10[kg]
5.85	43.40363	140.34793	(c)10[kg]
5.9	43.67593	142.53173	(c)10[kg]
5.95	43.94687	144.72907	(c)10[kg]
6	44.21646	146.93989	(c)10[kg]
6.05	44.48471	149.16413	(c)10[kg]
6.1	44.75161	151.40171	(c)10[kg]
6.15	45.01719	153.65257	(c)10[kg]
6.2	45.28145	155.91664	(c)10[kg]
6.25	45.54438	158.19386	(c)10[kg]
6.3	45.806	160.48416	(c)10[kg]
6.35	46.06632	162.78748	(c)10[kg]
6.4	46.32534	165.10374	(c)10[kg]
6.45	46.58307	167.4329	(c)10[kg]
6.5	46.83951	169.77487	(c)10[kg]
6.55	47.09468	172.12961	(c)10[kg]
6.6	47.34857	174.49704	(c)10[kg]
6.65	47.60119	176.8771	(c)10[kg]
6.7	47.85256	179.26972	(c)10[kg]
6.75	48.10267	181.67486	(c)10[kg]
6.8	48.35153	184.09243	(c)10[kg]
6.85	48.59916	186.52239	(c)10[kg]
6.9	48.84555	188.96467	(c)10[kg]
6.95	49.0907	191.4192	(c)10[kg]
7	49.33464	193.88594	(c)10[kg]
7.05	49.57736	196.3648	(c)10[kg]
7.1	49.81887	198.85575	(c)10[kg]
7.15	50.05917	201.35871	(c)10[kg]
7.2	50.29828	203.87362	(c)10[kg]
7.25	50.53619	206.40043	(c)10[kg]
7.3	50.77292	208.93908	(c)10[kg]
7.35	51.00847	211.4895	(c)10[kg]
7.4	51.24284	214.05164	(c)10[kg]
7.45	51.47604	216.62544	(c)10[kg]
7.5	51.70808	219.21085	(c)10[kg]
7.55	51.93896	221.80779	(c)10[kg]
7.6	52.16869	224.41623	(c)10[kg]
7.65	52.39727	227.03609	(c)10[kg]
7.7	52.62472	229.66733	(c)10[kg]
7.75	52.85103	232.30988	(c)10[kg]
7.8	53.07621	234.96369	(c)10[kg]
7.85	53.30027	237.6287	(c)10[kg]
7.9	53.52321	240.30486	(c)10[kg]
7.95	53.74504	242.99212	(c)10[kg]
8	53.96576	245.6904	(c)10[kg]
8.05	54.18538	248.39967	(c)10[kg]
8.1	54.40391	251.11987	(c)10[kg]
8.15	54.62135	253.85094	(c)10[kg]
8.2	54.8377	256.59282	(c)10[kg]
8.25	55.05297	259.34547	(c)10[kg]
8.3	55.26717	262.10883	(c)10[kg]
8.35	55.4803	264.88284	(c)10[kg]
8.4	55.69237	267.66746	(c)10[kg]
8.45	55.90338	270.46263	(c)10[kg]
8.5	56.11334	273.2683	(c)10[kg]
8.55	56.32225	276.08441	(c)10[kg]
8.6	56.53012	278.91092	(c)10[kg]
8.65	56.73695	281.74776	(c)10[kg]
8.7	56.94275	284.5949	(c)10[kg]
8.75	57.14752	287.45228	(c)10[kg]
8.8	57.35127	290.31984	(c)10[kg]
8.85	57.55401	293.19754	(c)10[kg]
8.9	57.75574	296.08533	(c)10[kg]
8.95	57.95646	298.98315	(c)10[kg]
9	58.15617	301.89096	(c)10[kg]
9.05	58.3549	304.8087	(c)10[kg]
9.1	58.55263	307.73634	(c)10[kg]
9.15	58.74937	310.6738	(c)10[kg]
9.2	58.94513	313.62106	(c)10[kg]
9.25	59.13992	316.57806	(c)10[kg]
9.3	59.33374	319.54474	(c)10[kg]
9.35	59.52659	322.52107	(c)10[kg]
9.4	59.71847	325.507	(c)10[kg]
9.45	59.9094	328.50247	(c)10[kg]
9.5	60.09938	331.50744	(c)10[kg]
9.55	60.28841	334.52186	(c)10[kg]
9.6	60.4765	337.54568	(c)10[kg]
9.65	60.66365	340.57886	(c)10[kg]
9.7	60.84986	343.62136	(c)10[kg]
9.75	61.03515	346.67311	(c)10[kg]
9.8	61.21951	349.73409	(c)10[kg]
9.85	61.40296	352.80424	(c)10[kg]
9.9	61.58548	355.88351	(c)10[kg]
9.95	61.7671	358.97187	(c)10[kg]
10	61.94781	362.06926	(c)10[kg]

同様に、X 軸 = t[s]、Y 軸 = v[m/s]、LEVEL = LEVEL[kg] としてプロットすると、空気抵抗の影響により、軽い物体ほど早く速度が頭打ちになり、重い物体ほど速い速度まで到達する様子が一目で分かります。

5. まとめ

空気抵抗がない場合、1kg・5kg・10kg の 3 水準を用意しても、グラフは完全に重なる
この「3 本重ねても同じ」という事実が、自由落下が重さに依存しないことの強い証拠になる
空気抵抗がある場合には、質量ごとに全く異なるカーブになり、重い物体ほど速く落ちるように見える
桜チャートと CSV データを組み合わせることで、こうした違いを授業やレポートで直感的に説明できる

本記事のサンプルデータを元に、抵抗係数や初速を変えたバージョンなど、オリジナルの自由落下シミュレーションを作ってみるのもおすすめです。

桜チャートホームへ戻る